On Sept. 13, starting at 11 A.M., mathematicians, musicians, and dancers will breathe life into the classic problem known as the Seven Bridges of Königsberg (7BK). The interactive exposition and performance celebrates this problem’s journey from 18th-century Prussia, in the small town of Königsberg, to 21st-century Atlanta.
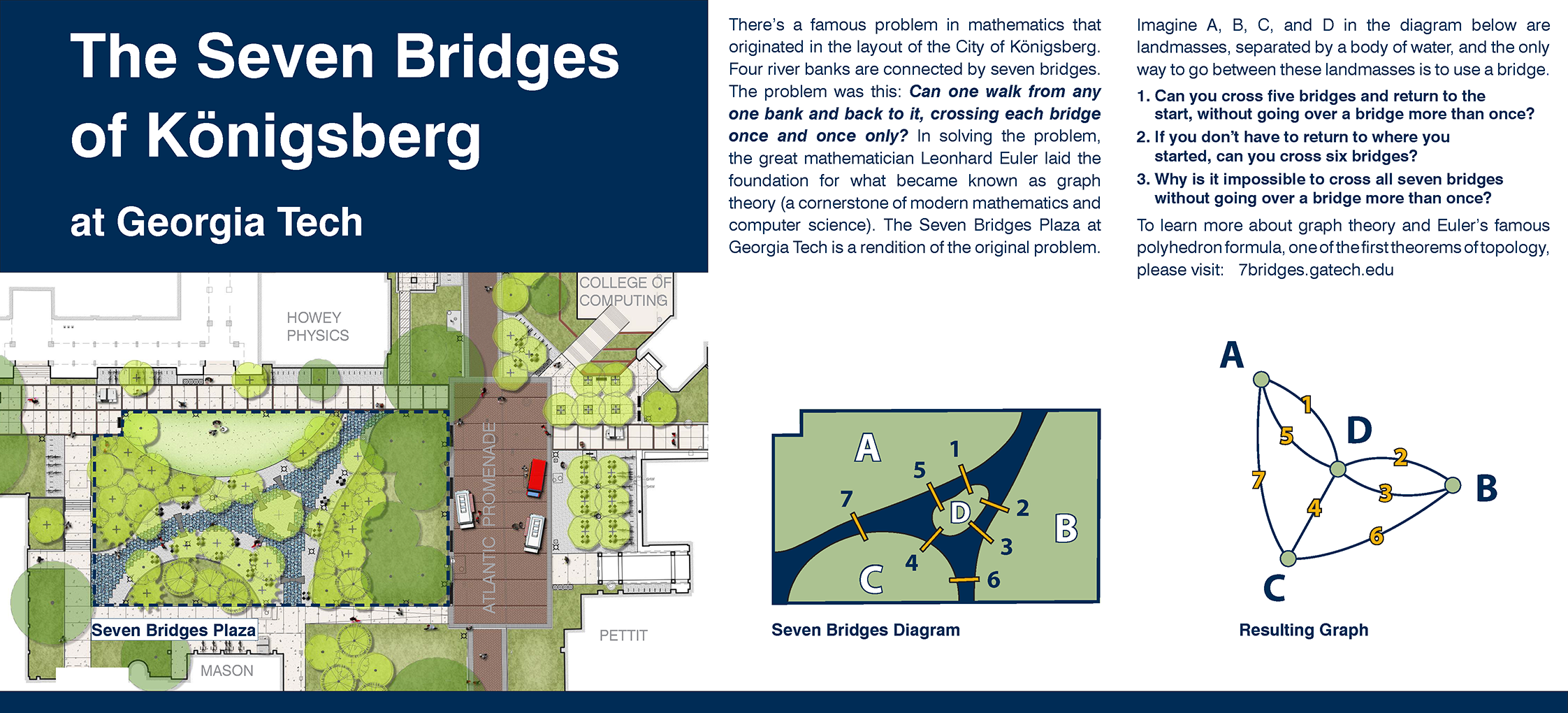
On the Georgia Tech campus is a representation of Königsberg and the seven bridges that connect its four land masses, which are divided by a river. The rendition – along the Atlantic Drive Promenade, on a site called the Seven Bridges Plaza – affirms that art, science, and mathematics are but different ways to grasp the world.
The Sept. 13 music and dance performance – The Seven Bridges of Königsberg – especially hopes to demystify and humanize mathematics, says Evans Harrell, an emeritus professor in the School of Mathematics.
The event begins with an interactive exposition by members of the Georgia Tech student organization Club Math. On each of the four land masses representing Königsberg, Club Math members will be at stations to discuss the 7BK problem; the life and times of Leonhard Euler, whose solution to the 7BK problem gave birth to graph theory; the role of graph theory in the modern world, and a special aspect of graph theory called the four-color theorem.
“Our project is also an experiment about how scientific stories can be told and about how the sciences can inspire original art.”
Euler, the Seven Bridges, and Graph Theory
The 7BK problem asks: Can one walk around Königsberg, crossing each of the seven bridges exactly once?
The Swiss mathematician Leonhard Euler proved that it is impossible to cross each of the seven bridges of Königsberg only once. The proof considered not only the case of Königsberg, but all possible ways a city could be connected by bridges and when it is possible to cross each bridge only once. In developing the proof, Euler invented a new field of mathematics, now called graph theory.
Euler’s insight was to simplify the problem, says Georgia Tech mathematics professor Dan Margalit. Graph theory reduces the problem to one about points – called vertices – and the lines – called edges – connecting them. The vertices correspond to the land masses and the edges are the bridges. The 7BK problem thus rendered, it is not hard to see the answer.
Margalit explains: Any attempted solution has two variations. In the first case, the journey starts and ends at the same land mass. Here, the number of bridges – or edges – associated with each land mass – or vertex – is even. Because every arrival at a land mass comes with a departure, every vertex has an even number of edges. Therefore any continuous path uses an even number of edges at each vertex. This is impossible in Königsberg because each land mass has an odd number of bridges.
In the second case, the journey ends in another place from where it started. Again the number of edges at each vertex must be even except at the start and end. Because to leave the start requires only one bridge, as does arriving at the end. Therefore, at the start and end vertices, the total number of edges will be an odd number. But at all other vertices, the number of edges would be even, as before.
Again this is impossible in Königsberg, because all the land masses have an odd number of bridges.
Graph theory permeates the modern world. “Facebook is a graph: vertices are people and edges are friendships," Margalit says. "Graph theory has many other applications all over science and mathematics."
“Facebook is a graph: vertices are people and edges are friendships.”
Math in Motion
For the Sept. 13 performance, Harrell partnered with the Georgia Tech School of Music’s Chaowen Ting. She will conduct the Georgia Tech Symphony Orchestra in performing original music by composer Marshall Coats. The music will accompany dances choreographed by artistic director Kristel Tedesco.
In a behind-the-scenes video, Tedesco says she recognized the similar struggles of mathematicians and artists working in imaginary worlds “and trying to find truth within them.” The resulting performance, she adds, aims to spark and stimulate the public’s curiosity about mathematics.
“We wish to engage the public in the wonder of mathematics and science, of music and dance, and the surprising ways that they can work together,” Harrell says. “Our project is also an experiment about how scientific stories can be told and about how the sciences can inspire original art.”
Support for the event came from Science in Vivo and Georgia Tech's College of Design, College of Sciences, and Office of the Arts.
For More Information Contact
A. Maureen Rouhi, Ph.D.
Director of Communications
College of Sciences