Download this episode
How can NASA stretch their fuel dollar for future missions to Jupiter and Saturn, and their potentially habitable moons? By using mathematical concepts that have been around for centuries. School of Mathematics Professor Rafael de la Llave is crunching the numbers for the space agency as it looks to save money during its next phase of exploration.
(Upbeat music)
Renay San Miguel:
Hello and welcome to ScienceMatters, the podcast of the Georgia Tech College of Sciences. I’m Renay San Miguel.
(Scene from “Interstellar”)
“Once we’ve gathered enough speed around Gargantua, we use Lander One and Ranger Two as rocket boosters to push us out of the black hole’s gravity.”
“Once Lander One has spent, Taurus will detach and get sucked right into that black hole.”
“Why does Taurus have to detach?”
“We have to shed the weight to escape the gravity.”
“Newton’s Third Law: The only way humans have ever figured how to get somewhere is to leave something behind.”
Renay San Miguel: Or, for every action, there is an equal and opposite reaction.
It can be argued that the best science fiction relies on science fact for its storytelling. In this case, it’s laws courtesy of Isaac Newton, the founder of modern physics.
The scene you just heard was from “Interstellar,” where astronauts rely on physics and math to escape the deathly gravity grip of a black hole.
(Scene from “The Martian”)
“I can get the Hermes back to Mars by Sol 561.”
“How?”
Renay San Miguel: Here’s the Oscar-nominated “The Martian” from 2015, as Donald Glover’s character uses a stapler to explain his plan to save stranded astronaut Matt Damon.
“Okay, let’s pretend that this stapler is the Hermes, and you are…I’m sorry, what’s your name again?”
“Teddy. I’m the director of NASA.”
“Right. Cool. Teddy. Now the Hermes is heading towards you, starting its month long deceleration and intercept, but instead what I’m proposing is --
(Makes rocket sounds with mouth)
“..we start accelerating immediately to preserve velocity and gain even more. We don’t intercept with Earth at all, but we come close enough to get a gravity assist and adjust course.”
“I’ve done the math. It checks out.”
Renay San Miguel: Rafael de la Llave, professor in the School of Mathematics, is doing the math for the real-life NASA.
Thanks to a 2018 space agency grant, he’s working on space flight solutions that aren’t that far removed from what Glover and “Interstellar’s” Matthew McConaughey use in their respective films.
De la Llave is studying how to use mathematics to save NASA fuel costs for future tours of the solar system’s outer planets, and its remote moons. More efficient spacecraft, using mathematics formulas that have been around for centuries, can save money and maybe get us to our destinations faster.
How?
Get ready to hear about Hamiltonian systems, Lagrange mechanics, Arnold diffusions. De la Llave is fluent in this kind of math talk.
Here’s the bottom line for what this could all mean for space flight, and for learning more about the planets and moons NASA wants to explore.
Rafael de la Llave: Well, one is that we can do much more daring missions, and then we can use significantly less fuel and we can also use—I mean, if you have a good understanding of the dynamical systems just by doing flybys, then you can find out things about, what is the gravitational field generated by the planets and then find out, for example, things about the composition. Do they have a hard cover or they are mainly gases or they have some structure inside et cetera? So all these things can be obtained thanks to having significantly better understanding of the mathematics.
(Upbeat music)
Renay San Miguel: To understand how math can help NASA fly more efficiently to other planets, whether with uncrewed space probes or crewed vehicles, we need to let de la Llave explain mathematical terms such as Lagrange mechanics and Hamiltonian systems.
Fortunately, de la Llave is considered to be one of the world’s experts in some of these systems, which combine math and physics.
Lagrange mechanics are what you use when classic Newtonian physics just aren’t enough for figuring out the paths of complicated systems like planets and their moons, and the gravitational forces they exert on each other and anything caught in those paths.
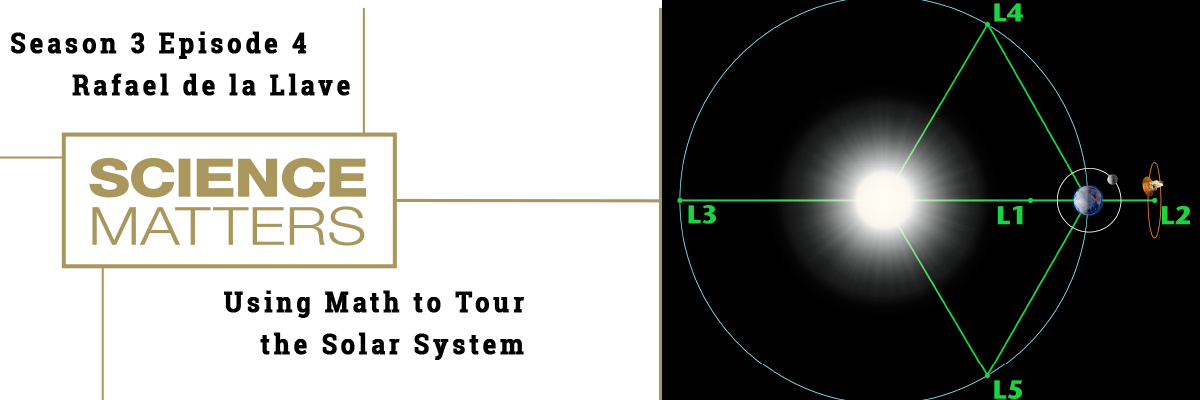
Rafael de la Llave: So Lagrange was a mathematician. He worked in France. So he discovered that if you have two massive bodies and then you put another small body, then the forces equilibrate at specifically at five points. So these are called the five Lagrange points. So three of them are in the line of the two bodies that are rotating and then two of them are in some equilateral points, et cetera. And so these places where the forces equilibrate are very interesting to the side maneuvers, because you can reach out of them. You more or less stop, and then you come back in a completely different direction. So that's the thing. So bouncing out of this is one of the things that people have discovered how to do now, and it's actually quite useful in many of—
Renay San Miguel: Use that Lagrange point as a way to maybe slingshot your way?
Rafael de la Llave: That's right. So you go to the Lagrange point, and then you more or less stop, and then you come back in a completely different direction. So this is the main thing.
Renay San Miguel: Next comes Hamiltonian systems, which is actually a subset of Lagrangian mechanics. It’s named after 19th-century Irish mathematician William Rowan Hamilton; not, you know, that other Hamilton guy.
This Hamilton brought together optics, mathematics, and physics to determine that light moved in waves. Hamiltonian mechanics help you figure out trajectories, or paths which have physical forces acting upon them. You’ll hear phase space mentioned and defined.
De la llave says Hamiltonian systems can help figure out the orbits of planets, and the orbits of atoms. Also, the velocities of objects, such as a target moon, and the probe we’ve sent its way, are now part of the equation.
Rafael de la Llave: Yes. So, Hamilton, this is a very interesting and very in my opinion defining study about this. So Hamilton was a mathematician in the 19th century and so he was working in optics and so he found a way of computing rays that moved from one place to another and how to design lenses. And then as an afterthought then he realized that the motion of rays in a medium is very similar to the motion of particles in phase space. So phase space is when you consider, not just the position, but also the velocity as a point in the space.
Renay San Miguel: Not just what what's out there, but how fast they’re moving?
Rafael de la Llave: But how fast it’s moving, exactly. Because if you look at it, Newton's laws prescribe the acceleration, which is how the velocity is changing, right? So in order to have a fixed initial condition, then you have the position and the velocity. So Hamilton discovered that if you consider the positions and the velocity, then the problem of mechanics is very similar to optics in twice the number of dimensions.
And then this led to very, very efficient calculations, because he could explain many constellations that people haven’t found by trial and error and painstakingly, then he could do them systematically and then you could do systematically many of the calculations that astronomers were doing and over a much-valued range of time. So—and actually this became a unifying point of mechanics and physics and optics and many other things.
Renay San Miguel: Again, interdisciplinary actions here involving math and physics—mathematicians and physicists working together.
Rafael de la Llave: And engineers.
Renay San Miguel: And engineers.
Rafael de la Llave: Don’t forget the engineers and even chemists. We have a—we have a grant with the European Union to find precisely developments in the mathematics of chemistry. So that’s—I mean, if you think a little bit about it, atoms bouncing is very similar to planets moving around and then the mathematics can be used from both problems.
Renay San Miguel: Yeah, it's all orbits, right?
Rafael de la Llave: It’s all orbits and so on, and yes, and very specific things. So it's a little bit more fun and—you get many more strange phenomenon in chemistry, because in chemistry all the—all the atoms of hydrogen are exactly the same. And then this allows you many more of these things that we call resonances, which is when two things have the same frequency, then very interesting phenomena start to happen. This is what drives much of the research that I am doing and much of the new phenomena that happens when two things have the same frequency then they can start transferring energy. This happens much more in chemistry than in celestial mechanics, because all the atoms tend to be identical.
(Upbeat music)
Renay San Miguel: Finally, there’s Arnold diffusion. The best way to describe this is a pendulum setup that de la Llave uses to show the waves and patterns tracked by this math concept.
Fifteen ball bearings hang by descending lengths of thread, from shortest to longest. A board is used to slightly lift all the bearings at the same time and set them swinging in unison. But it takes just a second for a major snake-like wave to establish itself in the bearings’ movements. Then wild patterns oscillate before the original pattern returns.
Arnold diffusion helps scientists figure out the patterns and pathways required to travel long distances to rendezvous with celestial bodies while dodging gravitational forces. Small moves can have big effects over time.
Also, De la Llave again mentions resonances, this time as a possible way to leap-frog our way to distant planets and moons.
Rafael De la Llave: But it’s this reason that you can have small effects, but they accumulate. The issue is the following: You have small effects and the issue is whether they average out and so on, or they start accumulating and lead to very large effects, et cetera.
There is this configuration in space, which we call “resonances.” So when the frequencies have more or less the same or a multiple to another, then things start to enhance and transfer energy and the effects start to accumulate. And now, the trick that people are discovering now how to do these days is that you can—so you go into a resonance, then lots of things happen, and then you get spit out. But you can arrange it in such a way that after you get spit out, then you land in another resonance and then the process continues. So this is a very interesting phenomenon, because it happens only in four dimensions. So you have to imagine four or five or six dimensions.
So there is this business that you can actually get the effect that drives you out of a resonance and then you manage to land into another one and then you can keep on bouncing from [indistinct] That's more or less Arnold diffusion.
Renay San Miguel: Arnold diffusion—small amounts of force can equal large effects over time.
Rafael de la Llave: That's correct.
Renay San Miguel: And so those—do you need a lot of force to make these resonances resonate?
Rafael de la Llave: No. No, that's the thing. We try to do these things with arbitrarily small forces. That's the thing. Yes.
Renay San Miguel: OK. All right.
Rafael de la Llave: I mean, if you put a little bit of eccentricity in these bodies and you have the Lagrange points, then you can get arbitrarily—you can get large effects and—but the eccentricities could be like 10 to the minus 50, 10 to the minus 100, 10 to the minus 1 million, whatever it is, then they will accumulate over time.
Renay San Miguel: So you figure all that into the engine burns of these ships as they're traversing these points, and you don't have to spend as much fuel.
Rafael de la Llave: Yes, so the mathematics is when you don't put any burns whatsoever. But there is a price to pay, which is that you have to spend a lot of time. But it’s for free. So if you're willing to spend a very, very large amount of time and how to do it for—we know how to do it for free. If you have less time, then this is the thing that we are working on now to put burns in such a way that you can do the same things that mathematicians know how to do for free. You're spending a little bit of fuel but in a reasonable amount of time.
(Upbeat music)
Renay San Miguel: De la Llave is originally from Spain, but left more than four decades ago to get his Ph.D. at Princeton. Despite his interest in orbital dynamics and the quickest, most efficient ways to visit planets, that part of math wasn’t always his priority.
Rafael de la Llave: No. I mean, I started in quantum field theory and statistical mechanics and so on. I mean, if you look at my collection of books, there is kind of a lot of things from quantum field theory to computers to statistical physics to…
Renay San Miguel: Just math. You just liked math?
Rafael de la Llave: Yes, and especially if it has connections with physics or with applications.
Renay San Miguel: OK. All right, because that's when you start thinking about the wider picture of how space is involved.
Rafael de la Llave: Yeah, I like that things that are related to something concrete and so on. I'm not very good at maintaining interest if it's just self-generated.
Renay San Miguel: You want to know how this applies to the things—the problems that you're trying to help NASA solve.
Rafael de la Llave: Yeah, these sort of things.
Renay San Miguel: It's just—I mean, did you always have a gift for math? I mean—or is that something that you really had to work on?
Rafael de la Llave: I don't think I have a gift, no. If I knew—I mean, I try.
Renay San Miguel: Because there's so many—I mean, a lot of people are afraid of math. A lot of folks come in and they have this anxiety about math. I've talked about this with some other people here about how you would go about getting younger people, like in K through 12 grades, interested in math and tell them how important it is and how much fun it could be.
Rafael de la Llave: Yes. Well, I think that math is basically thinking carefully about something that you care about. And if you think carefully, then this is math. So you don't fool yourself in making false steps or making extra assumptions. And if you're doing this, then you think about anything that you care about and you to try to think about carefully and then you're doing math.
Renay San Miguel: And you will find math showing up in other scientific disciplines, like physics, like as you said chemistry
Rafael de la Llave: Biology is a very new thing, and we don't know much about it, et cetera, but you have many things like combinatorics, et cetera come into biology and so on. And then there is also things like logistics, how to move things from one place to another using the least amount of effort, et cetera. I mean, Georgia Tech has always been a leader in that.
(Upbeat music)
Renay San Miguel: My thanks to Rafael de la Llave, professor in the School of Mathematics, for helping to explain Hamiltonian systems and Arnold diffusion.
Also thanks to 20th Century Fox, Legendary Pictures, Paramount Pictures, and Warner Brothers for the film clips.
Siyan Zhou, a former research associate with the School of Psychology, composed our theme music.
If you enjoyed this podcast, please subscribe. We’re on Apple Podcasts and Soundcloud.
This is ScienceMatters, the podcast of the Georgia Tech College of Sciences. I’m Renay San Miguel. Thanks for listening.
(Upbeat music)